Cadenas de Markov

CADENAS DE MARKOV

 

 
Las cadenas de Markov son modelos probbilísticos que se usan para predecir la evolución y el comportamiento a corto y largo plazo de determinados sistemas. Deben su nombre al matemático ruso Andrei Markov.

 
ANDREI MARKOV

Andréi Andréyevich Márkov (Андре́й Андре́евич Ма́рков) (14 de junio de 1856 - 20 de julio de1922) fue un matemático ruso conocido por sus trabajos en la teoría de los números y la teoría de probabilidades. Pertenecio a la escuela matematica de San Petersburgo fundada por Chebychev, y junto a Liapunov llego a ser una de las figuras mas eminentes de la misma en el campo de la probabilidad. Sin duda la otra contribución importante de Markov fue la introduccion del concepto de cadena
Sus primeras contribuciones son relativas al teorema central del límite para variables independientes pero no identicamente distribuidas y son motivadas por una imprecision que había cometido Chebychev y que Markov corrige.
de Markov, como un modelo para el estudio de variables dependientes, el cual dio lugar a una gran cantidad de investigacion posterior en la teoría de los procesos estocásticos.
 
DEFINICIÓN DE CADENA DE MARKOV
 
Una cadena de Markov es un proceso estocástico con un número finito de estados con probabilidades de trancisión estacionarias, es decir, si se conoce la historia del sistema hasta su instante actual, su estado presente resume toda la información relevante para describir en probabilidad su estado futuro.

Una cadena de Markov es una secuencia X1, X2, X3,..., de variables aleatorias. El rango de estas variables, es llamado espacio estado, el valor de Xn es el estado del proceso en el tiempo n. Si la distribución de probabilidad condicional de Xn+1 en estados pasados es una función de Xn por si sola, entonces:
Prob{Xn+1=j|X0=k0, X1=k1, ..., Xn-1=kn-1, Xn=i}= Prob{Xn+1=j|Xt=1}
Donde Xi es el estado del proceso en el instante i. La identidad mostrada es la Propiedad de Markov.
ELEMENTOS Y PROPIEDADES DE LAS CADENAS DE MARKOV
Toda cadena de Markov tiene los siguientes elementos: 
  1. Un conjunto finito de M estados, exhaustivos y mutuamente excluyentes (ejemplo: estados de la enfermedad)
  2. Ciclo de markov (“paso”) : periodo de tiempo que sirve de base para examinar las transiciones entre estados (ejemplo, un mes)
  3. Probabilidades de transición entre estados, en un ciclo (matriz P)
  4. Distribución inicial del sistema entre los M estados posibles.
Toda cadena de Markov cumple con las siguientes propiedades:
  • Propiedad Markoviana:
Un proceso estocástico tiene la propiedad markoviana si las probabilidades de transición en un paso sólo dependen del estado del sistema en el período anterior (memoria limitada).
P{Xt+1=j| Xt=i}=Pij

 
  • Las probabilidades son estacionarias:
P{Xt+1=j| Xt=i}=P{X1=j|X0=i}=Pij
P{Xt+n=j| Xt=i}=P{Xn=j|X0=i}=Pij^(n)

 
  • Existe un conjunto de probabilidades iniciales:
P{X0=i}

 
  • Existe una matriz de transición:
La matriz de transición es aquella que contiene todas las probabilidades de transición.
Las probabilidades de transición indican la probabilidad de que partiendo de un estado i se llegue al estado j en n períodos.

 
P(n)es la matriz de transición en n pasos, de orden (M+1)x(M+1)
 
Cálculo de Probabilidades de Transición en n pasos:
 
Cálculo de Vector de Probabilidades no condicionadas
 
TIPOS DE ESTADOS
 

 
 
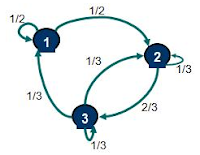
Si existe una probabilidad no nula que comenzando en un estado i se pueda llegar a un estado j al cabo de un cierto número de etapas (digamos n) se afirma que el estado j es accesible desde el estado i. Si consideramos el ejemplo 1 podemos afirmar que el estado 3 es accesible desde el estado 1. Aún cuando en una etapa no podemos llegar desde el estado 1 al estado 3, si podemos hacerlo al cabo de 2, 3, ..., n etapas. Cabe destacar en este punto que es relevante que exista una probabilidad no nula que comenzando en 1 se pueda llegar a 3 al cabo de un cierto número de etapas no importando el valor exacto de esta probabilidad para un n cualquiera. En cuanto al ejemplo 2, se puede verificar que el estado 2 es accesible desde el estado 3, sin embargo, el estado 2 no es accesible desde el estado 4 (esto porque una vez que se llega al estado 4 no se sale de ese estado). Finalmente, dos estados que son accesibles viceversa se dice que se comunican y que pertenecen a una misma clase de estados.
 
Una Cadena de Markov donde todos sus estados son accesibles entre sí y por tanto se comunican se dice que es irreducible, es decir, que existe una únicaclase de estados. Este es el caso del ejemplo 1.
 
En cambio si al menos existen 2 clases de estados la cadena ya no es irreducible. Si tenemos 2 estados que no se comunican (esto porque no son accesibles viceversa) estos estados perteneceran a distintas clases de estados. En el ejemplo 2 existen 3 clases de estados {0}, {1,2,3}, {4} (en consecuencia no es una cadena irreducible). En cuanto al estado 0 y estado 4, estos son estados absorbentes debido a que una vez que se accede a ellos la probabilidad de seguir en ese estado es de un 100%. Un estado absorbente define una clase de estados por si mismo.

 
Una definición adicional es la periodicidad de un estado. Un estado se dice que tiene periodo d, para el mayor valor entero de d que cumpla:
 
 
 
sólo para valores de n pertenecientes al conjunto {d, 2d, 3d, ....}. Si d=1 decimos que el estado es aperiódico. En otras palabras, un estado es periódico si, partiendo de ese estado, sólo es posible volver a él en un número de etapas que sea múltiplo de un cierto número entero mayor que uno
 
En el ejemplo 1 todos los estados son aperiódicos. En el ejemplo 2 los estados 1, 2 y 3 son periódicos con periodo d=2, es decir, que comenzando, por ejemplo, en el estado 1, la probabilidad de volver al mismo estado es sólo no nula para una cierta cantidad de pasos o etapas múltiplo de 2.
 
Un estado es recurrente en la medida que comenzando en él se tenga la certeza de volver en algun momento del tiempo (una determinada cantidad de etapas) sobre si mismo. Alternativamente, un estado es transciente si no se tiene la certeza de volver sobre si mismo. En el ejemplo 1 todos los estados son recurrentes. En el ejemplo 2 los estados 1, 2 y 3 son transcientes debido a que si se comienza en cualquiera de ellos no se puede asegurar con certeza que se volverá al mismo estado en algún momento (esto debido a que existe una probabilidad no nula de acceder a un estado absorbente: 0 o 4). Los estados absorbentes por definición son estados recurrentes.
 
Si tenemos una Cadena de Markov que tiene una cantidad finita de estados e identificamos un estado recurrente, este será recurrente positivo. Si la cantidad de estados es infinito entonces un estado recurrente será recurrente nulo.

 
CADENAS ABSORBENTES

 
Un estado tal que si el proceso entra en él permanecerá indefinidamente en este estado (ya que las probabilidades de pasar a cualquiera de los otros son cero), se dice estado absorbente.
De una cadena de Markov que consta de estados transitorios y absorbentes se dice que es una cadena absorbente de Markov.
Si una cadena de Markov contiene algún estado absorbente, la línea de la matriz de transición correspondiente a las probabilidades de transición de dicho estado constará de un 1 en la diagonal principal y ceros en los demás elementos. Será por lo tanto una matriz no regular.
 
Para poder estudiar las cadenas de Markov absorbentes es preciso reordenar la matriz de transición de forma que las filas correspondientes a los estados absorbentes aparezcan en primer lugar. Así ordenada se dirá que la matriz de transición está en la forma canónica.
 
Donde:
I: Matriz Identidad
0: Matriz Nula
N: Matriz No Absorbente
A: Matriz Absorbente

El valor esperado se calcula como:
 
V. Esp=(I-N)^-1
 
La probabilidad de caer en los estados absorbentes se calcula como:
 
P=A*(I-N)^-1
 
 
Para más información visita....
 

 

 
Suscribirse a: Entradas (Atom)