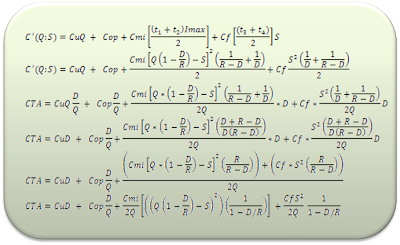GESTIÓN DE INVENTARIOS
CLASIFICAIÓN DE LOS INVENTARIOS
- Demanda dependiente: Es aquella que es causada por las necesidades de un semiterminado o un artículo de mas alto nivel en el proceso de valor agregado. Por ejemplo: las llantas, los motores, etc. son artículos cuyas necesidades dependen de la demanda de automóviles.
- Demanda independiente: Es aquella que surge a partir de decisiones ajenas a la empresa, es decir, es determinada directamente por las necesidades del mercado. Dentro de este grupo, es posible realizar una subdivisión: Demanda Independiente Constante y Demanda Independiente Variable.
Teniendo en cuenta la anterior clasificación, se ha procedido a agrupar los diferentes modelos de inventario de demanda dependiente que se han desarrollado.
MODELO GENERAL DE INVENTARIO
Una política de inventario se encarga de dar respuesta a dos interrogantes básicos: ¿Cuánto pedir? y ¿Cuándo pedir?. Para resolver tales cuestiones basta con hacer uso de una sencilla ecuación:

- El Costo de Compra se refiere al precio por unidad del artículo.
- El Costo de Preparación es el costo fijo incurrido cuando se coloca un pedido, este costo no tiene relación con la cantidad pedida.
- El Costo de Almacenamiento es el costo de mantener una existencia en el inventario.
- El Costo de Faltante es la penalización en la que se incurre cuando se terminan las existencias.
MODELOS DETERMINÍSTICOS DE INVENTARIO
Modelo de Calidad Económica de Pedido (CEP) o Modelo EOQ por sus siglas en inglés (Economic Order Quality), fue desarrollado por Ford Harris alrededor del año 1915. La función de este modelo es calcular la cantidad que debe pedirse o producirse minimizando los costos de colocación del pedido para inventario y los costos de manejo de inventario. El modelo EOQ se basa en los siguientes supuestos:
- La demanda es constante y conocida. La demanda de un producto no influye en la de otro.
- No existe incertidumbre en la demanda, la oferta y el tiempo de entrega. No se presenta agotamiento de existencias.
- Se genera un costo por mantener existencias en inventario.
- Cada vez que se coloca un pedido se incurre en un costo.
- Los costos por mantener existencias en inventario y por colocar pedidos no se ven afectados por el tamaño del pedido.
- La reposición es instantánea, no hay entregas parciales.
En base a los anteriores supuestos, se puede graficar el comportamiento de las cantidades en función del tiempo.
Niveles de inventario en un modelo EOQ sin faltante. |
Del anterior gráfico se deduce que Q son las cantidades del pedido, d es el índice de demanda y t es el tiempo.Teniendo en cuenta la ecuación que determina el costo total de inventario, se puede deducir una nueva ecuación basada en supuestos geométricos:
Es necesario expresar tal ecuación en función del tiempo, para esto se divide en ambos lados de la igualdad por la expresión correspondiente al tiempo:
Realizando las operaciones correspondientes a reducción de términos semejantes, se obtiene la siguiente ecuación final:
La anterior expresión determina el valor total por tiempo de unidad, pero como lo que se desea obtener es el valor óptimo de tal función, que se representa por el punto en que se interceptan el Costo por mantener existencias en el inventario (Cmi), el Costo por pedir (Cp) y la proyección del punto inferior de la curva que determina el Costo Total Anual (Ctanual).
Para obtener el punto óptimo, se procede a minimizar la función Costo Total Anual respecto a Q. Suponiendo que Q es continua, una condición necesaria para encontrar el valor óptimo es:
Teniendo esa condición presente, se procede a derivar la función y a realizar el despeje correspondiente para obtener el punto óptimo Q:
De la anterior ecuación se deduce que:
- Cuando la demanda es menor que la óptima, el costo de pedir es mayor que el costo de mantener existencias en el inventario.
- Si la demanda es la óptima, el costo de pedir y el de mantener en el inventario son iguales.
- Si la demanda es mayor que la óptima, el costo de pedir es menor que el costo de mantener existencias en el inventario.
MODELO EOQ CON FALTANTE
En este modelo se admiten todos los supuestos, anteriormente enunciados del EOQ, con la excepción de que en este caso, si se admiten faltantes. Es decir, si el cliente permite que su pedido se satisfaga algún tiempo después, en caso de que no se encuentre disponible algún artículo que éste haya solicitado, entonces la venta no se pierde. Bajo esta condición, el inventario puede reducirse, aunque los costos anuales de inventarios deben considerar entonces los costos por faltante.
Teniendo presente lo anterior, es posible graficar el comportamiento del inventario en una empresa de la siguiente forma:
Niveles de inventario en un Modelo EOQ sin flatante. |
Del anterior gráfico, se deduce que Q son las cantidades del pedido, t es el tiempo empleado en satisfacer tal pedido y S es el faltante en que se incurre al no satisfacer la totalidad del pedido. Teniendo en cuenta la ecuación que determina el costo total de inventario, se puede deducir una nueva expresión basada en supuestos geométricos.
La ecuación general para el costo total de inventario es:
De la anterior gráfica se deduce que:
Al reemplazar las anteriores expresiones en la ecuación general, se procede a deducir la nueva expresión que determinará el punto óptimo del modelo:
Es necesario expresar la ecuación en función del tiempo, por lo que se divide en ambos lados la de igualdad por el tiempo que se tarda en entregar un pedido:
Es necesario obtener el valor óptimo de Q y S, por lo cual se procede a derivar parcialmente la ecuación (6) con respecto a Q y a S. Además, se asume que el valor de esta derivada es igual a 0:
MODELO LEP SIN FALTANTE
Modelo de Lote Económico de Producción. En este modelo se considera que la tasa de producción (R) es mayor que la demanda (D) y se toma en cuenta que existe un costo por generar una orden de producción.En este caso se prohíben los faltantes estableciendo el costos por faltantes como infinito . Las condiciones para este aprovisionamiento instantáneo de los insumos se modifican ligeramente cuando los suministros se manufacturan al recibir la orden, en vez de que se surtan de existencias de artículos ya manufacturados.
Niveles de inventario en un Modelo LEP sin faltante |
Donde:
- t1 es el tiempo positivo de acción en fabricación
- t2 es el tiempo en el cual el inventario máximo llega a 0
- t = t1 + t2, es el tiempo total en el cual se está produciendo, es decir el tiempo entre corrida.
De la anterior gráfica se deduce que:
Tomando en cuenta la ecuación general para el costo total de inventario se procede a establecer una expresión que determine el óptimo para este modelo:
Para expresar la anterior ecuación en función del tiempo, se divide en ambos lados de la ecuación por la expresión que determina el tiempo en que es entregado un pedido. De dicha ecuación, se procede a derivar con respecto a Q con el fin de obtener el óptimo para el modelo:
MODELO LEP CON FALTANTE
Esta extensión de EOQ permite que existan faltantes y se cumplan las entregas atrasadas, suponiendo que exista un nivel mínimo de atraso que la administración este dispuesta a tolerar. Los faltantes ocurren en el sistema de producción por falta de material, falta de capacidad o ambas. En este modelo se consideran las siguientes variables:
- R: Tasa de producción
- D: Demanda
- Q: Cantidad de productos del pedido
- I: Inventario
- S: Faltante
- t1: Tiempo que transcurre desde que el inventario esta en 0 hasta alcanzar el inventario máximo.
- t2: Tiempo que transcurre en agotarse el inventario máximo.
- t1+t2: Tiempo que transcurre en agotarse las existencias.
- t3: Tiempo en el cual empieza a acumularse los pedidos pendientes.
- t4: Tiempo en el que se enciende la máquina y el sistema se nivela con los pedidos pendientes.
- t=t1+t2+t3+t4: Tiempo entre corridas.
Nievles de inventario en un Modelo LEP con faltante. |
De la gráfica anterior se pueden hacer ciertas deducciones geométricas tales como las que se muestran a continuación:
Aplicando la fórmula general del costo total de inventario, reemplazando las anteriores deducciones se obtiene la siguiente expresión:
Al derivar parcialmente con respecto a Q y a S, se obtiene el óptimo del modelo, que se encuentra representado por las siguientes expresiones:
MODELO EOQ PROBABILIZADOEl tamaño de las existencias estabilizadoras se determina de modo que la probabilidad de agotamiento de las existencias durante el tiempo de entrega (el periodo entre colocar y recibir un pedido) no exceda un valor predeterminado.
Sean:
L = tiempo de entrega entre colocar y recibir un pedido.
ðL = demanda promedio durante el tiempo de entrega.
σL = desviación standard de la demanda durante el tiempo de entrega.
B = tamaño de la existencia estabilizadora o stock de seguridad.
ð = máxima probabilidad disponible de agotamiento de las existencias durante el tiempo de entrega. (Distribución Normal)
XL = variable aleatoria que representa la demanda durante el tiempo de entrega.
Para más información visita...